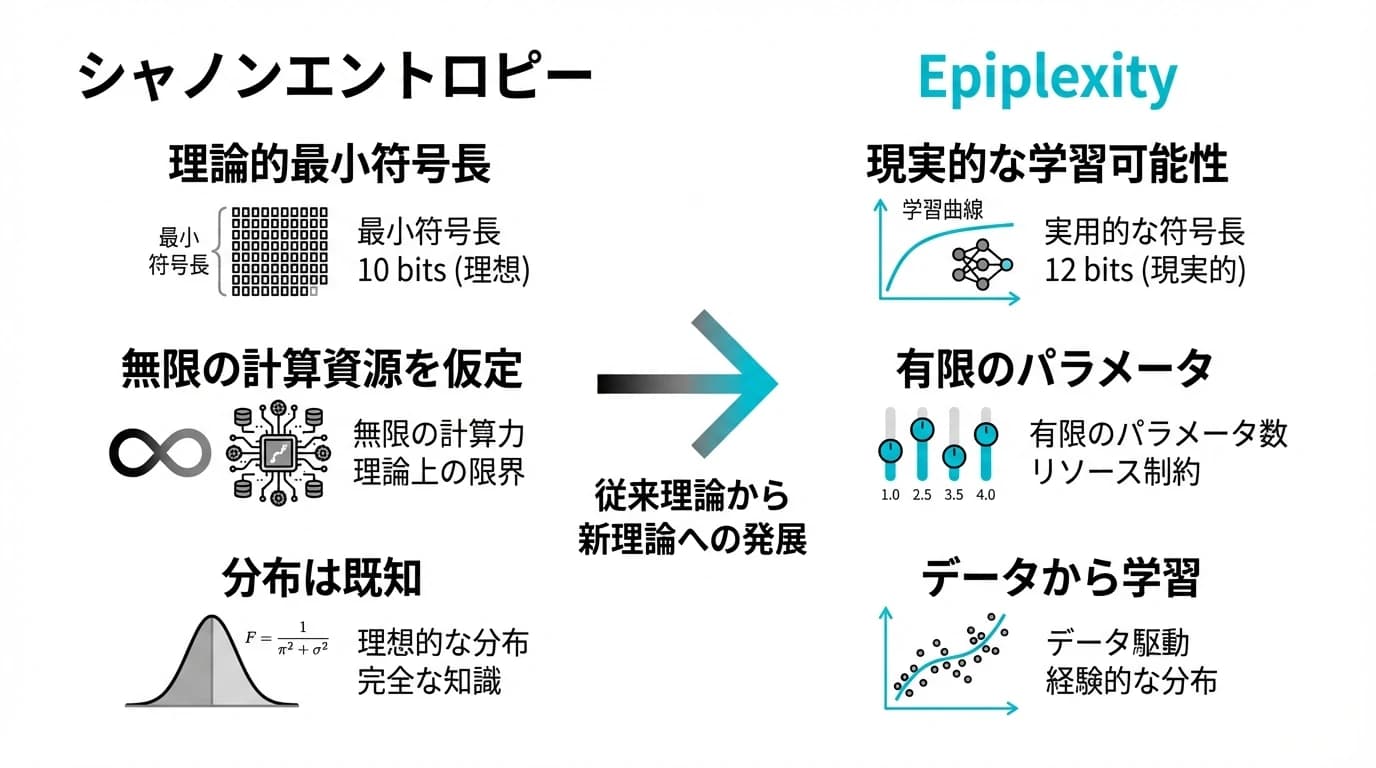
シャノンエントロピーは情報理論の基盤ですが、現実のAIモデルには「無限の計算資源」がありません。2026年にCMUとNYUの研究チームが発表した「Epiplexity（エピプレキシティ）」は、計算制約のあるモデルにとって何が学習可能かを定量化する新しい情報理論の尺度です。

本記事では、Epiplexity論文の内容を徹底解説し、従来の情報理論では説明できなかった3つのパラドックスをどう解決するかを明らかにします。

Epiplexityとは？3行でわかる論文の要点

1. 従来手法の課題: シャノンエントロピーは「無限の計算資源」を仮定しており、現実のAIモデルの学習を正しく評価できない
2. Epiplexityのアプローチ: 特定のモデルアーキテクチャと学習アルゴリズムを考慮した「学習可能な情報量」を定量化
3. なぜ重要か: Data Augmentation、Curriculum Learning、LLMの汎用能力など、従来説明できなかった現象を統一的に説明

論文情報

従来の情報理論の限界

シャノンエントロピーの前提

クロード・シャノンが1948年に提唱した情報理論は、理想的な符号化に基づいています。

H(X) = -Σ p(x) log p(x)

この数式は「データ X を完全に記述するために必要な最小ビット数」を表します。

しかし、シャノンエントロピーには重大な前提があります。

• 分布 p(x) が既知である
• 最適な符号を構築できる無限の計算資源がある
• 復号にも無限の計算資源がある

現実のAIモデルとのギャップ

実際のAIモデル（GPT、BERT、ResNetなど）には厳しい計算制約があります。

この乖離が、従来の情報理論では説明できない現象を生み出しています。

Epiplexityが解く3つのパラドックス

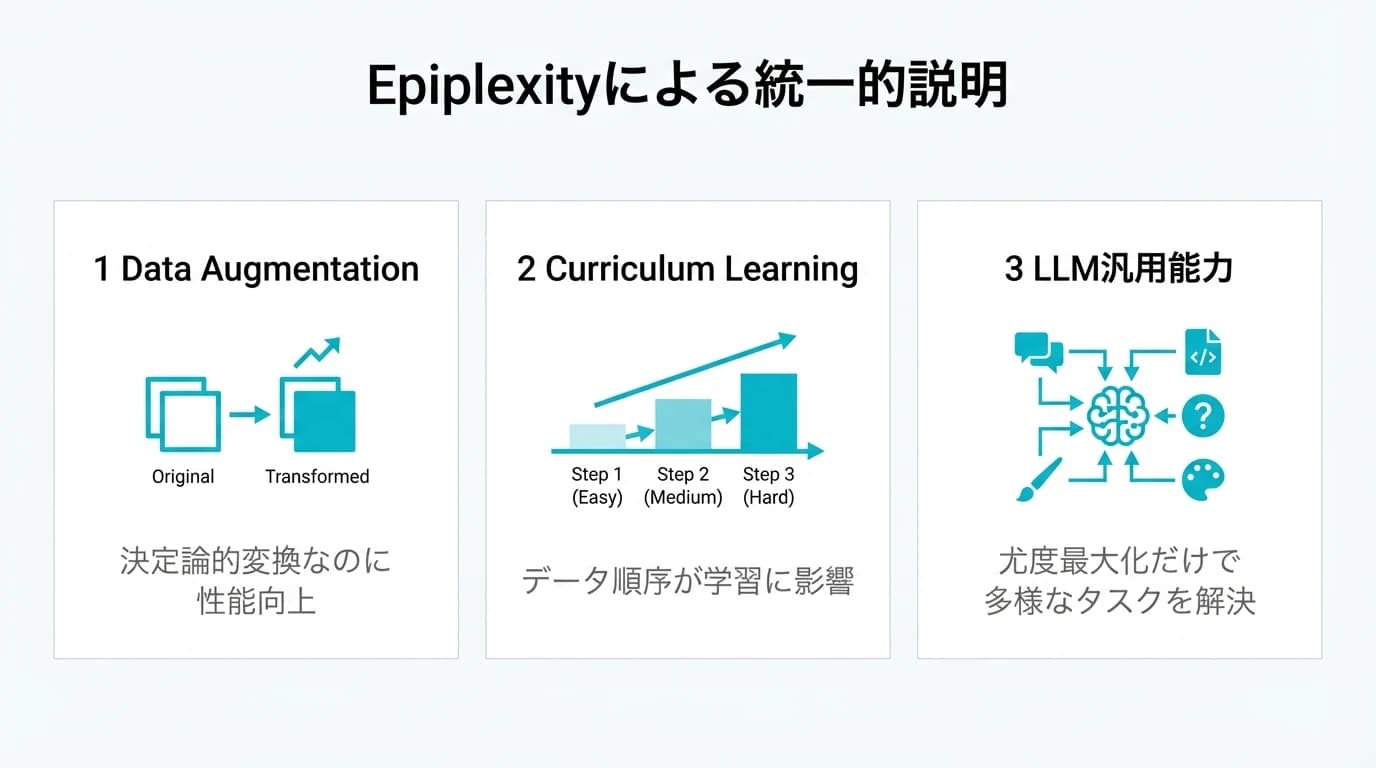
パラドックス1: 決定論的変換で情報が増加する

Data Augmentationは、画像を回転・反転・ノイズ付加することでモデルの精度を向上させる技術です。

元画像 → 回転・反転・ノイズ付加 → 拡張データ → モデル精度向上

従来の情報理論の説明:

決定論的変換では情報量は変化しない（むしろ減少）。H(f(X)) ≤ H(X)

現実:

Data Augmentationでモデル性能が大幅に向上する。

Epiplexityの説明:

変換によって「計算制約のあるモデルが学習可能な側面」が増加する。同じ情報量でも、モデルが利用しやすい形式に変換されている。

パラドックス2: データの順序が重要になる

Curriculum Learningは、簡単なデータから難しいデータへと学習順序を工夫する技術です。

簡単 → 普通 → 難しい → 高効率な学習

従来の情報理論の説明:

データ集合の情報量は順序に依存しない。

現実:

学習順序によって最終的なモデル性能が大きく変わる。

Epiplexityの説明:

SGD（確率的勾配降下法）を使うモデルにとって、データの順序は「いつ・どの情報を吸収できるか」に影響する。Epiplexityはこの順序依存性を捉える。

パラドックス3: 尤度モデリングは分布マッチング以上

LLMの事前学習は、次のトークンを予測する（尤度を最大化する）だけで、分類・生成・推論など多様なタスクで高性能を発揮します。

事前学習（尤度最大化） → 分類/生成/推論など複数の下流タスクで高性能

従来の情報理論の説明:

尤度モデリングは単に学習データの分布を再現しているだけ。

現実:

LLMは学習データにない新しいタスクも解ける（ゼロショット能力）。

Epiplexityの説明:

モデルは単なる分布マッチングではなく、構造的なパターンを学習している。Epiplexityは、この「構造化された学習」を正しく評価する。

Epiplexityの定義

Prequential Coding

Epiplexityの中核はPrequential（Predictive Sequential）Codingという符号化方式です。

def prequential_codelength(data, model, learning_algorithm):
    """
    データをオンラインで圧縮しながら学習する
    """
    total_codelength = 0

    for i, x_i in enumerate(data):
        # 現在のモデルでx_iを予測
        prob = model.predict_probability(x_i)
        codelength = -log(prob)
        total_codelength += codelength

        # モデルを更新
        model = learning_algorithm.update(model, x_i)

    return total_codelength

この符号長の期待値がEpiplexityです。

数式定義

データ分布 P、モデルアーキテクチャ M、学習アルゴリズム A に対して、Epiplexityは次のように定義されます：

Epiplexity(P | M, A) = E[Σ -log p_θ_t(x_{t+1})]

ここで θ_t は、データ x_1, ..., x_t を学習した後のモデルパラメータです。

エントロピーとの関係

重要な性質：Epiplexity ≥ Entropy

どんなモデル・アルゴリズムを使っても、シャノンエントロピー以下にはなりません。

実験結果と実用性

データ選択への応用

論文では、Epiplexityを使ったデータ選択が下流タスクの性能と強く相関することを示しています。

実験設定:

• 様々なデータセットに対してEpiplexityを計算
• 同じデータセットで学習したモデルの下流タスク性能を測定
• Epiplexityと性能の相関を分析

結果:

Epiplexityが低い（＝効率的に学習できる）データセットほど、下流タスクでの性能が高い傾向。

OOD汎化との関係

EpiplexityはOut-of-Distribution（OOD）汎化とも関連します。

• Epiplexityが低いデータで学習 → 構造的パターンを効率的に学習
• 構造的パターンは新しいドメインでも有効
• 結果としてOOD性能が向上

AI開発への示唆

データセット設計の新しい指針

Epiplexityの観点から、良いデータセットとは：

1. モデルが学習しやすい形式: 生データより前処理・拡張されたデータ
2. 適切な順序: 簡単から難しいへのカリキュラム構造
3. 構造的多様性: 単なる量より、学習可能なパターンの多様性

事前学習の最適化

LLMの事前学習において、Epiplexityは以下の最適化に使える可能性があります：

• データミックス比率の決定
• 学習順序（カリキュラム）の設計
• データ品質の評価指標

今後の研究方向

• 大規模言語モデルでのEpiplexity計算の効率化
• Epiplexityに基づくデータ選択アルゴリズムの開発
• 他のアーキテクチャ（Vision Transformer等）への適用

FAQ

Q1. Epiplexityは実際に計算できる？

はい、Prequential Codingに基づいて計算可能です。ただし、大規模なデータセット・モデルでは計算コストが高くなります。論文では効率的な近似手法も提案されています。

Q2. エントロピーはもう使わない方がいい？

いいえ。エントロピーは依然として重要な理論的下限を与えます。Epiplexityは「実用的な学習可能性」を評価する補完的な指標として使うのが適切です。

Q3. Data Augmentationの効果を予測できる？

理論的には可能です。変換前後のEpiplexityを比較することで、その変換がモデルの学習にどう影響するか予測できる可能性があります。

Q4. 日本語LLMにも適用できる？

はい。Epiplexityは言語に依存しない一般的な枠組みです。日本語データセットの評価にも使えます。

まとめ

Epiplexityは、計算制約のあるAIモデルにとって何が学習可能かを定量化する新しい情報理論の尺度です。

主な貢献:

• 従来の情報理論では説明できなかった3つのパラドックスを統一的に解決
• Data Augmentation、Curriculum Learning、LLMの汎用能力の理論的説明を提供
• データセット設計の新しい指針を提示

実践のポイント:

• データの「量」より「学習しやすさ」が重要
• 学習順序（カリキュラム）がモデル性能に影響
• Epiplexityはデータ選択の新しい指標になりうる

情報理論とAI研究の橋渡しとして、Epiplexityは今後の発展が期待される重要な概念です。

関連記事

参考リソース

• arXiv論文
• シャノンの情報理論（Wikipedia）
• Data Augmentation解説
• Curriculum Learning論文

本記事はネクサフローのAI研究シリーズの一部です。